Una solución estadística para la crisis de la replicación en ciencia [Publicado originalmente en The Conversation en Octubre/2017]

Por Valen E. Johnson

Imagen: mario_luengo / Freepik

En un ensayo de un nuevo medicamento para curar el cáncer, el 44 por ciento de 50 pacientes lograron la remisión después del tratamiento. Sin el medicamente, sólo el 32 por ciento de pacientes anteriores hicieron lo mismo. El nuevo tratamiento parece prometedor, pero ¿es mejor que el estándar?

Esta pregunta es difícil, por lo que los estadísticos tienden a responder una pregunta diferente. Miran sus resultados y calculan algo llamado valor-p. Si el valor-p es menor que 0,05, los resultados son “estadísticamente significativos” – en otras palabras, es poco probable que sean causados por la casualidad.

El problema es que muchos resultados estadísticamente significativos no son replicables. Un tratamiento que parece prometedor en un ensayo no muestra ningún beneficio en absoluto cuando se administra al siguiente grupo de pacientes. Este problema se ha vuelto tan severo que una revista de psicología realmente prohibió por completo los valores-p.

Mis colegas y yo hemos estudiado este problema, y creemos que sabemos lo que lo está causando. La barrera para reclamar significación estadística simplemente es demasiado baja.

La mayoría de las hipótesis son falsas

La Open Science Collaboration, una organización sin fines de lucro enfocada en la investigación científica, intentó replicar 100 experimentos de psicología publicados. Mientras que 97 de los experimentos iniciales informaron hallazgos estadísticamente significativos, sólo 36 de los estudios replicados sí lo hicieron.

Varios estudiantes de posgrado y yo usamos estos datos para estimar la probabilidad de que un experimento de psicología elegido al azar pruebe un efecto real. Descubrimos que solo un 7 por ciento lo hace. En un estudio similar¹, la economista Anna Dreber y sus colegas estimaron que solo el 9 por ciento de los experimentos se replicarían.

Ambos análisis sugieren que sólo uno en 13 nuevos tratamientos experimentales en psicología – y probablemente en muchas otras ciencias sociales – resultarán ser un éxito.

Esto tiene implicaciones importantes a la hora de interpretar valores-p, particularmente cuando están cerca de 0,05.

El factor de Bayes

Los valores-p cercanos a 0,05 tienen más probabilidades de ser debidos a una probabilidad aleatoria de lo que la mayoría de la gente cree. Para entender el problema, regresemos a nuestro ensayo imaginario del medicamento. Recuerde, 22 de 50 pacientes con el nuevo medicamento entraron en remisión, en comparación con un promedio de sólo 16 pacientes de 50 con el tratamiento anterior.

La probabilidad de ver 22 o más éxitos de 50 es 0,05 si el nuevo medicamento no es mejor que el anterior. Esto significa que el valor-p para este experimento es estadísticamente significativo. Pero queremos saber si el nuevo tratamiento realmente es una mejora, o si no es mejor que la forma anterior de hacer las cosas.

Para averiguarlo, debemos combinar la información contenida en los datos con la información disponible antes de realizar el experimento, o las “probabilidades previas”. Las probabilidades anteriores reflejan factores que no se miden directamente en el estudio. Por ejemplo, podrían explicar el hecho de que en otros 10 ensayos con medicamentos similares, ninguno resultó exitoso.

Si el nuevo medicamento no es mejor que el anterior, entonces las estadísticas nos dicen que la probabilidad de ver exactamente 22 de 50 éxitos en este ensayo es 0,0235 – relativamente bajo.

¿Qué pasa si el nuevo medicamento es en realidad mejor? En realidad no conocemos la tasa de éxito del nuevo medicamento, pero creemos que está cerca de la tasa de éxito observada, 22 en 50. Si asumimos eso, entonces la probabilidad de observar 22 éxitos en 50 es 0,0113 – aproximadamente 5 veces más probable. (No es casi 20 veces más probable, sin embargo, como se podría adivinar si supiera que el valor-p del experimento era 0,05).

Este ratio de probabilidades se llama factor Bayes. Podemos usar el teorema de Bayes para combinar el factor de Bayes con las probabilidades anteriores para calcular la probabilidad de que el nuevo tratamiento sea mejor.

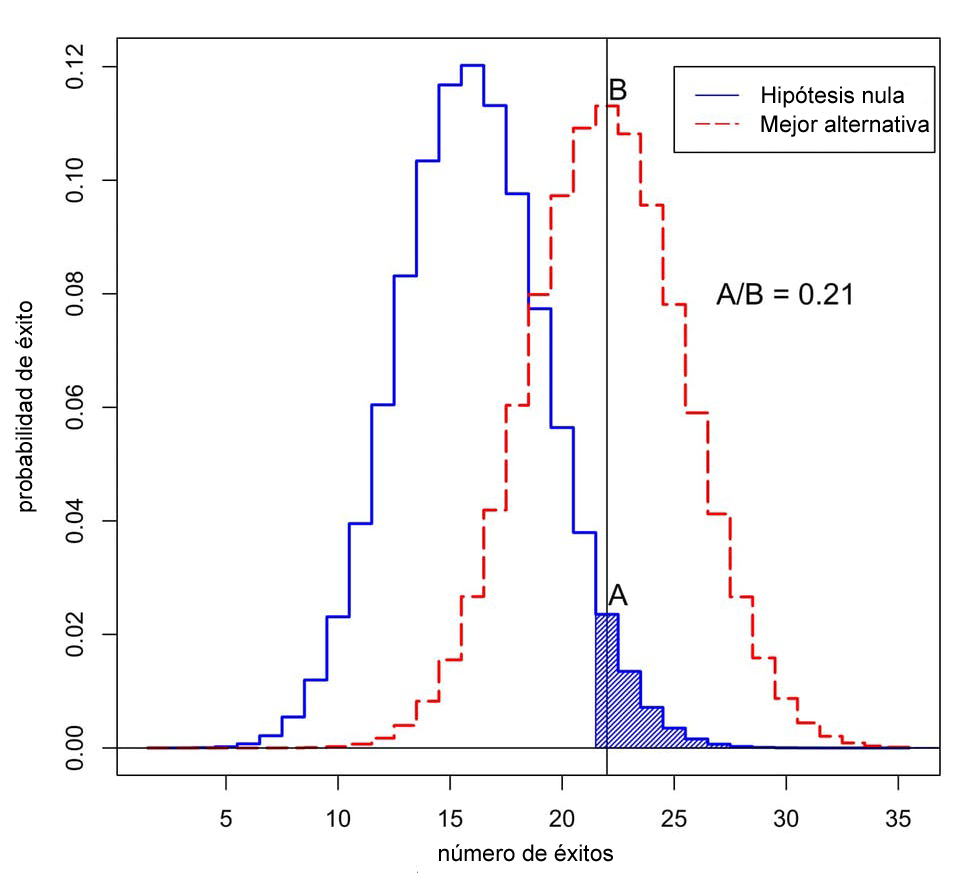
Adaptado de lo original: Valen Johnson

¿Cuál es la probabilidad de observar el éxito en 50 ensayos? La curva azul representa las probabilidades bajo la “hipótesis nula”, cuando el nuevo tratamiento no es mejor que el anterior. La curva roja representa las probabilidades cuando el nuevo tratamiento es mejor. El área sombreada representa el valor-p. En este caso, el ratio de probabilidades asignado a 22 éxitos es A dividido por B, o sea 0.21.

Por el bien del argumento, supongamos que solo 1 de cada 13 tratamientos experimentales contra el cáncer será un éxito. Eso está cerca del valor que estimamos para los experimentos de psicología.

Cuando combinamos estas probabilidades anteriores con el factor de Bayes, resulta que la probabilidad de que el nuevo tratamiento sea mejor que el anterior es al menos 0,71. ¡Pero el valor-p estadísticamente significativo de 0,05 sugiere exactamente lo contrario!

Un nuevo enfoque

Esta inconsistencia es típica de muchos estudios científicos. Es particularmente común para valores-p cercanos a 0,05. Esto explica por qué una alta proporción de resultados estadísticamente significativos no replican.

Entonces, ¿cómo debemos evaluar las afirmaciones iniciales de un descubrimiento científico? En septiembre, mis colegas y yo propusimos una nueva idea: sólo los valores-p mejores a 0,005 deberían ser considerados estadísticamente significativos. Valores-p entre 0,005 y 0,05 simplemente deberían llamarse sugestivos.

En nuestra propuesta, los resultados estadísticamente significativos es más probable que se repliquen, incluso después de tener en cuenta las pequeñas probabilidades previas que normalmente corresponden a los estudios en las ciencias sociales, biológicas y médicas.

Además, creemos que la significación estadística no debería servir como un umbral de línea brillante para la publicación. Los resultados estadísticamente sugestivos – o incluso los resultados que son en gran medida no concluyentes – también podrían publicarse, en función de si informan o no la evidencia preliminar importante con respecto a la posibilidad que una nueva teoría sea cierta.

El 11 de octubre presentamos esta idea a un grupo de estadísticos en el Simposio ASA sobre Inferencia Estadística en Bethesda, Maryland. Nuestro objetivo al cambiar la definición de significación estadística es restablecer el significado previsto de este término: que los datos han proporcionado un apoyo sustancial para un descubrimiento científico o efecto de tratamiento.

Crítica de nuestra idea

No todos están de acuerdo con nuestra propuesta, incluyendo otro grupo de científicos dirigidos por el psicólogo Daniel Lakens.

Argumentan que la definición de los factores de Bayes es demasiada subjetiva, y que los investigadores pueden hacer otras suposiciones que podrían cambiar sus conclusiones. En el ensayo clínico, por ejemplo, Lakens podría argumentar que los investigadores podrían informar la tasa de remisión a los tres meses en lugar de a los seis meses, si proporciona evidencia más sólida en favor del nuevo medicamento.

Lakens y su grupo también consideran que la estimación de que sólo uno de cada 13 experimentos se replicará es demasiado baja. Señalan que este cálculo no incluye efectos como p-hacking, un término usado cuando los investigadores analizan repetidamente sus datos hasta que encuentran un valor-p fuerte.

En lugar de elevar la barrera de la significación estadística, el grupo de Lakens cree que los investigadores deberían establecer su propio nivel de significación estadística antes de realizar sus experimentos.

Estoy en desacuerdo con muchas de las afirmaciones del grupo de Lakens y, desde una perspectiva puramente práctica, siento que su propuesta es imposible. La mayoría de las revistas científicas no proporcionan un mecanismo para que los investigadores registren y justifiquen su elección de los valores-p antes de realizar experimentos. Lo que es más importante, permitir que los investigadores establezcan sus propios umbrales de evidencia no parece una buena manera de mejorar la reproducibilidad de la investigación científica.

La propuesta de Lakens solo funcionaría si los editores de revistas y las agencias de financiación acordaran por adelantado en publicar informes de experimentos que no se hayan realizado según los criterios impuestos por los propios investigadores a sí mismos. Creo que es poco probable que esto suceda en algún momento del futuro cercano.

Hasta que esto ocurra, yo recomiendo que no confíe en las aseveraciones de estudios científicos basados en valores-p cercanos a 0,05. Insista en estándares más elevados.

Nota

1. DREBER, A., et al. Using prediction markets to estimate the reproducibility of scientific research. Proceedings of the National Academy of Sciences [online]. 2015, vol. 112, no. 50, pp. 15343-15347 [viewed 18 October 2017]. DOI: 10.1073/pnas.1516179112. Available from: http://www.pnas.org/content/112/50/15343

Referências

American Statistical Association releases statement on statistical significance and p-values [online]. American Statistical Association (ASA). 2016 [viewed 18 October 2017]. Available from: http://www.amstat.org/asa/files/pdfs/P-ValueStatement.pdf

BENJAMIN, D. J., et al. Redefine statistical significance. Nature Human Behaviour [online]. 2017 [viewed 18 October 2017]. DOI: 10.1038/s41562-017-0189-z. Available from: https://www.nature.com/articles/s41562-017-0189-z

DREBER, A., et al. Using prediction markets to estimate the reproducibility of scientific research. Proceedings of the National Academy of Sciences [online]. 2015, vol. 112, no. 50, pp. 15343-15347 [viewed 18 October 2017]. DOI: 10.1073/pnas.1516179112. Available from: http://www.pnas.org/content/112/50/15343

HEAD, M. L. The Extent and Consequences of P-Hacking in Science. PLOS Biology [online]. 2015, vol. 13, no. 3, e1002106 [viewed 18 October 2017]. DOI: 10.1371/journal.pbio.1002106. Available from: http://journals.plos.org/plosbiology/article?id=10.1371/journal.pbio.1002106

JOHNSON, V. E. Revised standards for statistical evidence. Proceedings of the National Academy of Sciences [online]. 2013, vol. 110, no. 48, pp. 19313-19317 [viewed 18 October 2017]. DOI: 10.1073/pnas.1313476110. Available from: http://www.pnas.org/content/110/48/19313

JOHNSON, V. E., et al. On the Reproducibility of Psychological Science. Journal of the American Statistical Association [online]. 2017, vol. 112, no. 517, ISSN: 1537-274X [viewed 18 October 2017]. DOI: 10.1080/01621459.2016.1240079. Available from: http://www.tandfonline.com/doi/full/10.1080/01621459.2016.1240079

LAKENS, D., et al. Justify Your Alpha: A Response to “Redefine Statistical Significance”. PsyArXiv Preprints [online]. 2017 [viewed 18 October 2017]. DOI: 10.17605/OSF.IO/9S3Y6. Available from: https://psyarxiv.com/9s3y6/

McGRAYNE, S. B. The Theory That Would Not Die: How Bayes’ Rule Cracked the Enigma Code, Hunted Down Russian Submarines, & Emerged Triumphant. New Haven: Yale University Press, 2012.

WOOLSTON, C. Psychology journal bans P values [online]. Nature. 2015 [viewed 18 October 2017]. Available from: http://www.nature.com/news/psychology-journal-bans-p-values-1.17001

Articulo original em inglés

https://theconversation.com/a-statistical-fix-for-the-replication-crisis-in-science-84896

Traducido del original en inglés por Ernesto Spinak.