Por Valen E. Johnson
Imagem: mario_luengo / Freepik
Em um experimento com uma nova droga para curar câncer, 44% dos 50 pacientes obtiveram remissão após o tratamento. Sem a droga, apenas 32% dos pacientes atingiram o mesmo resultado. O novo tratamento parece promissor, mas é melhor do que o padrão?
Esta questão é difícil, então os estatísticos tendem a responder a uma pergunta diferente. Eles examinam seus resultados e calculam algo chamado valor-p. Se o valor-p for inferior a 0,05, os resultados são “estatisticamente significativos” – em outras palavras, é improvável terem sido causados apenas por chance aleatória.
O problema é que muitos resultados estatisticamente significativos não estão sendo replicados. Um tratamento que se mostra promissor em um ensaio não mostra qualquer benefício quando administrado ao próximo grupo de pacientes. Este problema tornou-se tão grave que um periódico de psicologia proibiu completamente os valores-p.
Meus colegas e eu estudamos este problema, e achamos que sabemos o que está causando isso. O limite para reivindicar significância estatística é simplesmente muito baixo.
A maioria das hipóteses é falsa
A Open Science Collaboration, uma organização sem fins lucrativos focada em pesquisa científica, tentou replicar 100 experimentos publicados de psicologia. Enquanto 97 dos experimentos iniciais relataram resultados estatisticamente significativos, apenas 36 dos estudos replicados obtiveram esses resultados.
Vários estudantes de pós-graduação e eu usamos estes dados para estimar a probabilidade de que um experimento de psicologia escolhido aleatoriamente tivesse um efeito real testado. Descobrimos que apenas cerca de 7% tiveram. Em um estudo semelhante1, a economista Anna Dreber e seus colegas estimaram que apenas 9% dos experimentos são replicáveis.
Ambas análises sugerem que apenas cerca de um em cada 13 novos tratamentos experimentais em psicologia – e provavelmente de muitas outras ciências sociais – acabará sendo um sucesso.
Isso tem implicações importantes ao interpretar valores-p, particularmente quando eles são próximos de 0,05.
O fator de Bayes
Valores-p próximos a 0,05 acontecem mais devido a fatores aleatórios do que imagina a maioria das pessoas.
Para entender o problema, voltemos ao nosso teste de drogas imaginário. Lembre-se, 22 dos 50 pacientes com o novo medicamento entraram em remissão, em comparação com a média de apenas 16 dos 50 pacientes no tratamento antigo.
A probabilidade de ver 22 ou mais sucessos entre 50 é de 0,05 se o novo medicamento não for melhor do que o antigo. Isso significa que o valor-p para este experimento é estatisticamente significativo. Mas queremos saber se o novo tratamento é realmente uma melhoria, ou se não é melhor do que a maneira antiga de fazer as coisas.
Para descobrir, precisamos combinar a informação contida nos dados com a informação disponível antes da realização do experimento, ou as “probabilidades anteriores”. As probabilidades anteriores refletem fatores que não são diretamente medidos no estudo. Por exemplo, eles podem explicar o fato de que em 10 outros testes de drogas similares, nenhum provou ser bem-sucedido.
Se a nova droga não for melhor do que a droga antiga, então as estatísticas nos dizem que a probabilidade de ver exatamente 22 entre 50 sucessos neste teste é 0,0235 – ou seja, relativamente baixa.
E se a nova droga realmente for melhor? Nós realmente não conhecemos a taxa de sucesso da nova droga, mas um bom palpite é que está perto da taxa de sucesso observada, 22 entre 50. Se assumirmos que, então, a probabilidade de observar exatamente 22 entre 50 sucessos é 0,113 – cerca de cinco vezes mais provável. (Não é quase 20 vezes mais provável, no entanto, como se poderia imaginar sabendo que o valor-p do experimento foi de 0,05.)
Esta relação de probabilidades é denominada fator de Bayes. Podemos usar o Teorema de Bayes para combinar o fator de Bayes com as probabilidades anteriores para calcular a probabilidade de que o novo tratamento seja melhor.
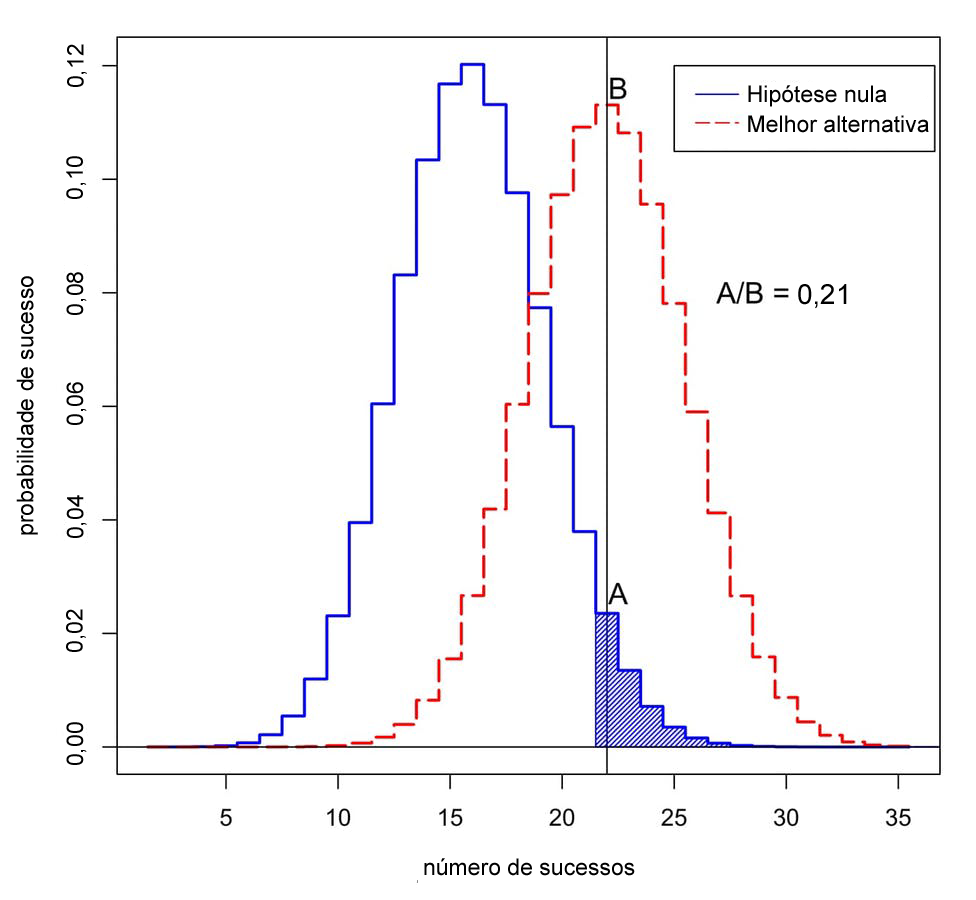
Adaptado do original: Valen Johnson
Qual a probabilidade de observar o sucesso em 50 ensaios? A curva azul representa probabilidades sob a “hipótese nula”, quando o novo tratamento não é melhor do que o antigo. A curva vermelha representa probabilidades quando o novo tratamento é melhor. A área sombreada representa o valor-p. Neste caso, a proporção das probabilidades atribuídas a 22 sucessos é A dividido por B, ou 0,21.
Por razões de argumentação, suponhamos que apenas 1 a cada 13 tratamentos experimentais de câncer virá a ser um sucesso. Isso é próximo ao valor que estimamos para as experiências de psicologia.
Quando combinamos estas probabilidades anteriores com o fator de Bayes, verifica-se que a probabilidade de que o novo tratamento não seja melhor que o antigo é de pelo menos 0,71. Mas o valor-p estatisticamente significativo de 0,05 sugere exatamente o oposto!
Uma nova abordagem
Esta inconsistência é típica de muitos estudos científicos. É particularmente comum para valores-p em torno de 0,05. Isso explica por que uma proporção tão alta de resultados estatisticamente significativos não pode ser replicada.
Então, como devemos avaliar as alegações iniciais de uma descoberta científica? Em setembro, meus colegas e eu propusemos uma nova ideia: Somente os valores-p inferiores a 0,005 devem ser considerados estatisticamente significativos. Os valores-p entre 0,005 e 0,05 devem ser chamados de sugestivos.
Em nossa proposta, resultados estatisticamente significativos são mais propensos a ser replicados, mesmo depois de explicar as pequenas probabilidades anteriores que geralmente pertencem a estudos nas ciências sociais, biológicas e médicas.
Além disso, consideramos que a significância estatística não deve servir como um limite padrão para publicação. Os resultados estatisticamente sugestivos – ou mesmo os resultados que são, em grande parte, inconclusivos – também podem ser publicados, baseados no fato de que eles relatam evidências preliminares importantes sobre a possibilidade de uma nova teoria vir a ser verdadeira ou não.
Em 11 de outubro de 2017, apresentamos esta ideia a um grupo de estatísticos no ASA Symposium on Statistical Inference em Bethesda, Maryland, EUA. Nosso objetivo ao mudar a definição de significância estatística é restaurar o significado pretendido deste termo: que os dados fornecidos forneçam suporte substancial para uma descoberta científica ou efeito de algum tratamento.
Críticas à nossa ideia
Nem todos concordam com a nossa proposta, incluindo outro grupo de cientistas liderados pelo psicólogo Daniel Lakens.
Eles argumentam que a definição dos fatores de Bayes é muito subjetiva e que os pesquisadores podem fazer outras alegações que podem mudar suas conclusões. Em ensaios clínicos, por exemplo, Lakens pode argumentar que os pesquisadores poderiam relatar a taxa de remissão de três meses ao invés de seis meses, caso fosse possível fornecer evidências mais fortes a favor da nova droga.
Lakens e seu grupo também consideram que a estimativa de que apenas cerca de um em cada 13 experimentos será replicado é muito baixa. Eles ressaltam que essa estimativa não inclui efeitos como p-hacking, um termo usado quando os pesquisadores analisam repetidamente seus dados até encontrarem um valor-p forte.
Em vez de aumentar o limiar para significância estatística, o grupo Lakens considera que os pesquisadores devem estabelecer e justificar seu próprio nível de significância estatística antes de realizar seus experimentos.
Eu discordo de muitas das reivindicações do grupo Lakens – e, de uma perspectiva puramente prática, acredito que sua proposta está fadada ao fracasso. A maioria dos periódicos científicos não fornece um mecanismo para que os pesquisadores possam registrar e justificar sua escolha de valores-p antes de realizar os experimentos. Mais importante ainda, permitir que os pesquisadores estabeleçam seus próprios limiares de evidências não parece ser uma boa maneira de melhorar a reprodutibilidade da pesquisa científica.
A proposta de Lakens só funcionaria se os editores de periódicos e as agências de fomento concordassem antecipadamente em publicar relatos de experimentos que não foram conduzidos com base em critérios que os próprios cientistas impuseram. Acho improvável que isso aconteça em qualquer momento no futuro próximo.
Até que isso aconteça, recomendo que não se confie em afirmações de estudos científicos com base em valores-p próximos de 0,05. Insista em padrões mais elevados.
Nota
1. DREBER, A., et al. Using prediction markets to estimate the reproducibility of scientific research. Proceedings of the National Academy of Sciences [online]. 2015, vol. 112, no. 50, pp. 15343-15347 [viewed 18 October 2017]. DOI: 10.1073/pnas.1516179112. Available from: http://www.pnas.org/content/112/50/15343
Referências
American Statistical Association releases statement on statistical significance and p-values [online]. American Statistical Association (ASA). 2016 [viewed 18 October 2017]. Available from: http://www.amstat.org/asa/files/pdfs/P-ValueStatement.pdf
BENJAMIN, D. J., et al. Redefine statistical significance. Nature Human Behaviour [online]. 2017 [viewed 18 October 2017]. DOI: 10.1038/s41562-017-0189-z. Available from: https://www.nature.com/articles/s41562-017-0189-z
DREBER, A., et al. Using prediction markets to estimate the reproducibility of scientific research. Proceedings of the National Academy of Sciences [online]. 2015, vol. 112, no. 50, pp. 15343-15347 [viewed 18 October 2017]. DOI: 10.1073/pnas.1516179112. Available from: http://www.pnas.org/content/112/50/15343
HEAD, M. L. The Extent and Consequences of P-Hacking in Science. PLOS Biology [online]. 2015, vol. 13, no. 3, e1002106 [viewed 18 October 2017]. DOI: 10.1371/journal.pbio.1002106. Available from: http://journals.plos.org/plosbiology/article?id=10.1371/journal.pbio.1002106
JOHNSON, V. E. Revised standards for statistical evidence. Proceedings of the National Academy of Sciences [online]. 2013, vol. 110, no. 48, pp. 19313-19317 [viewed 18 October 2017]. DOI: 10.1073/pnas.1313476110. Available from: http://www.pnas.org/content/110/48/19313
JOHNSON, V. E., et al. On the Reproducibility of Psychological Science. Journal of the American Statistical Association [online]. 2017, vol. 112, no. 517, ISSN: 1537-274X [viewed 18 October 2017]. DOI: 10.1080/01621459.2016.1240079. Available from: http://www.tandfonline.com/doi/full/10.1080/01621459.2016.1240079
LAKENS, D., et al. Justify Your Alpha: A Response to “Redefine Statistical Significance”. PsyArXiv Preprints [online]. 2017 [viewed 18 October 2017]. DOI: 10.17605/OSF.IO/9S3Y6. Available from: https://psyarxiv.com/9s3y6/
McGRAYNE, S. B. The Theory That Would Not Die: How Bayes’ Rule Cracked the Enigma Code, Hunted Down Russian Submarines, & Emerged Triumphant. New Haven: Yale University Press, 2012.
WOOLSTON, C. Psychology journal bans P values [online]. Nature. 2015 [viewed 18 October 2017]. Available from: http://www.nature.com/news/psychology-journal-bans-p-values-1.17001
Artigo original em inglês:
https://theconversation.com/a-statistical-fix-for-the-replication-crisis-in-science-84896
Traduzido do original em inglês por Lilian Nassi-Calò.
Como citar este post [ISO 690/2010]:




![É preciso um corpo para entender o mundo – por que o ChatGPT e outras IAs de linguagem não sabem o que dizem [Publicado originalmente no The Conversation em abril/2023] Fotografia de um robô branco e prateado segurando um tablet na frente de uma loja de malas de viagem. Ao fundo, no corredor, duas pessoas estão caminhando de costas para a câmera.](https://blog.scielo.org/wp-content/uploads/2023/04/lukas-hND1OG3q67k-unsplash_thumb.jpg)
![A falta de planos de sustentabilidade para serviços de preprints põe em risco o seu potencial para aprimorar a ciência [Publicado originalmente no LSE Impact Blog em março/2023] Fotografia de um servidor de rede.](https://blog.scielo.org/wp-content/uploads/2023/03/taylor-vick-M5tzZtFCOfs-unsplash_thumb.jpg)
![eLife encerra decisões de aceitar/rejeitar após avaliação por pares [Publicado originalmente pela eLife em outubro/22] Logo da eLife](https://blog.scielo.org/wp-content/uploads/2022/11/eLife-logo_thumb.jpg)
![O Santo Graal não existe: workshops de OPERAS-P e OASPA para publishers sobre modelos inovadores de negócios para livros [Publicado originalmente no OAPEN Blog em julho/2021] holy_grail_thumb](https://blog.scielo.org/wp-content/uploads/2021/07/holy_grail_thumb.png)
![Post convidado – Construindo um caminho mais fácil para a publicação de livros em acesso aberto: Apoio para autores [Publicado originalmente no Scholarly Kitchen em março/2021] Post convidado – Construindo um caminho mais fácil para a publicação de livros em acesso aberto: Apoio para autores [Publicado originalmente no Scholarly Kitchen em março/2021]](https://blog.scielo.org/wp-content/uploads/2021/12/iStock-1263424631-1024x683_thumb.jpg)







Últimos comentários